Multi-digit Multiplication

When I teach multi-digit multiplication to my 4th and 5th graders, I present it in many different ways, sometimes to the dismay of parents and other teachers. They say, “Why don’t you teach them the way we have always done it?” (Meaning the standard algorithm.) “It worked fine for me!” And it does work fine, if the students can memorize and retain it. But teaching the other methods first—place value sections, expanded notation, and algebraic notation—allows students to develop better understanding of why we do what we do. And more times than not, they remember it and make fewer mistakes.

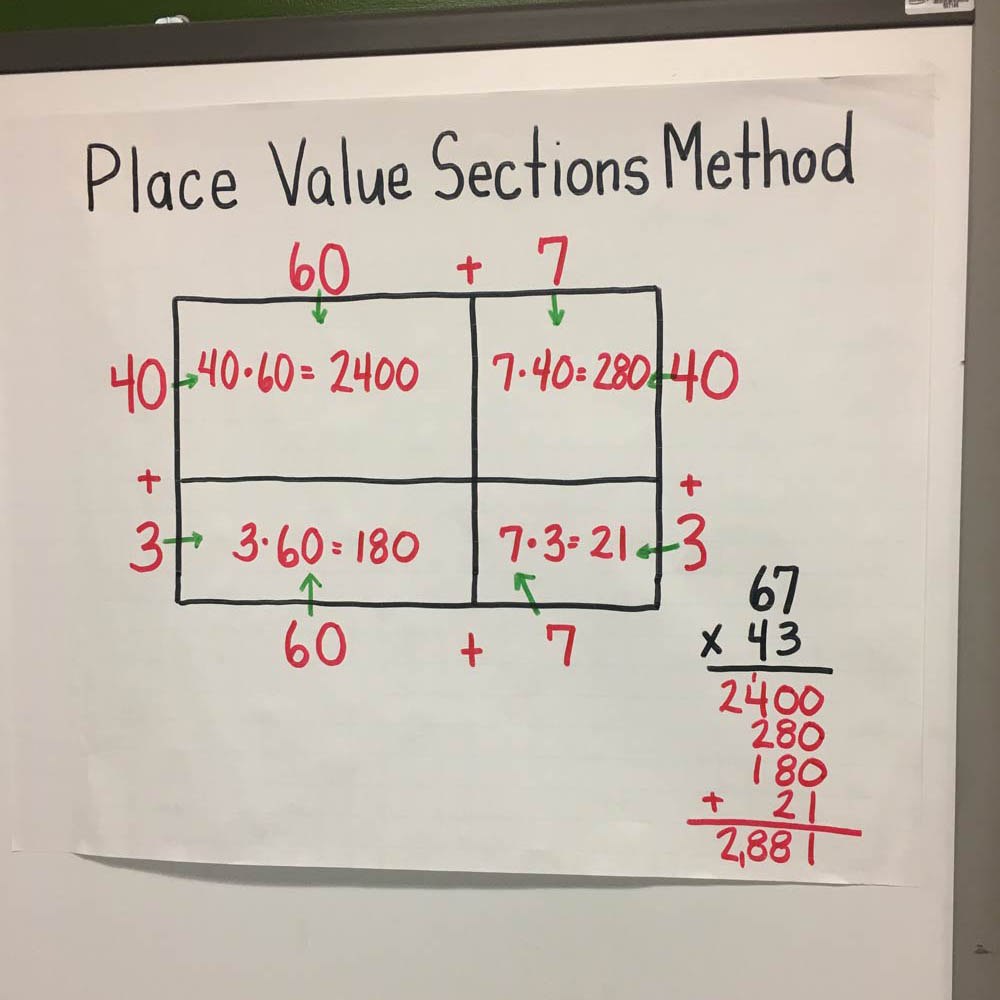
The first method we learn is the place value sections method (see image 1), which we also call the area model. This method works very well, emphasizing place value of the numbers through expanded form and multiplying by powers of 10. In addition, it really uses the formula for area of a rectangle by multiplying L X W for each of the interior rectangles. We use this for 1 digit x 4 digit, and 2 digit x 2 digit, but some of my 5th grade students also use it for 2 digit x 3 digit or multiplication of decimals.

Once students understand that method, some move to expanded notation method (see image 2). Students find it is similar to the first method, but it does not use the rectangle. It is slightly more advanced, so not all the students use it, but it is effective and makes sense. The numbers are still expanded, then multiplied by each other number. In 2 digit x 2 digit, the four products are the same as the four found using the place value sections method, then added together.

Then, some of the students will move to using the algebraic notation method (see image 3). This is a great way to demonstrate the distributive property, or what will later be called the FOIL method when solving binomials. Not many of my students will choose this method, but I do show it to them. They usually think it is pretty cool.

Once we have worked through all three of those methods, I show them the shortcut method or the standard algorithm (see image 4). We stress why we use the zero placeholder when we multiply the second digit in the tens place, and not just memorize the steps. By the end of 5th grade, most of the students are using the shortcut method, but a few will use one of the other methods, which is fine with me. I always say, as long as you get the right answer, use the method that works best for you!